Excel-ing In Life
Personal finance is full of unknowns. There always seem to be these looming questions around “what if this happens” or “what will that look like in the future”. It’s hard to know all the answers definitively, but we can make estimates which can help guide our decisions. When it comes to quantitative or numbers based questions, one of the best tools to do this Excel. Here are my two favorite formulas in excel and how to implement them into your personal finances.
Paying Off Loans (=PMT)
The first, and likely the most popular, is the Payment (=PMT). With this, you’re able to calculate what your total payment amount is on a loan with just three pieces of information: Loan total, how many years it’s for, and the annual interest rate (in excel these bits of information are called ‘arguments’). To figure out what information is needed for an excel function, you can begin the function, in this case ‘=pmt’ into any cell and the below image will populate. This black box reflects all arguments you need to have before you can execute the function.
For payment we need:
Rate - Annual interest rate
Nper - Number of periods or payments
Pv - Present value of the loan
[Fv] - Future value of the loan
[Type] - An input of 0 or 1 which is only used when calculating annuity payments
Every excel function has arguments that are listed in abbreviated terms like these. If you ever get stuck, the excel help function explains in detail what each argument is asking for. This is what the payment function looks like in the help section.
The best way to visualize setting up a problem is to create a column with titles on the left and the corresponding information on the right. As you can see here below, I’ve created a mock table for a 30 year fixed rate home loan of $200,000 at 3.5%. Cell B6 shows the exact formula that is written to calculate the payment in cell B5.
Because the first argument, rate, refers to a monthly rate (you make monthly payments on mortgages), you need to divide the annual interest rate by 12 which gives you what percent rate you’re paying each month. You don’t have to calculate this - the function figures it out for you. The second argument, nper, wants the number of payments being made over the course of the loan. As we established we are making monthly payments, you need to multiply the loan year length by 12 to get total payments. Lastly, we put the total loan amount. In this particular function, future value and the last argument are optional - I have the future value set to zero (because your loan total is zero at the end of the loan) but isn’t required.
*A noteworthy point - once you have the payment calculated, you can multiply that number by the total number of payments to get the total amount paid. In this example, 30 years of $898.09 mortgage payments equate to a total paid of $323,312.18. Yikes
Interest & Principal
If you really want to nerd out, you’re able to calculate specifics in paying off your loans as well. At any given payment in a loan, you’re paying a portion of interest and a portion of principal. As you get closer to the end of the life of the loan, you’re paying more towards the initial principal than just interest. With a modification of the payment function, you’re able to calculate how much you pay towards interest and how much you pay towards principal at any specific payment. Using ‘=ipmt’ or ‘=ppmt’ you’re able to determine how much you are paying in interest or principal respectively.
Saving for Vacation?
While this context is used to figure out the payments to pay off a loan, you can also use this function to figure out how much you would need to save to reach a certain goal. Let’s say you need to save $1000 for a vacation in six months, the payment function could tell you how much to save to reach it. If the money was in cash and not earning interest, the rate would be zero. The number of payments would reflect the number of times to contribute, say every paycheck between now and when you leave. The present value would be zero or whatever amount you have saved up already and the future value would be whatever the end goal amount is.
Value of Future Investments (=FV)
One of the most encouraging things to think about is estimating the value of your savings or investments. We all want to know what we’re working towards right? The future value formula allows you to find the value of an investment in the future based on a savings or interest rate.
Here is the same concept as payment - input the rate of return expected on your investment, how many periods it will compound, the amount of money added in payments, and the present value of your money. Similar to the payment function, care needs to be taken when using the rate of return and the number of periods. If you’re using an annual return rate, the number of periods should be in years. If the return is monthly, the return period should be measured in months.
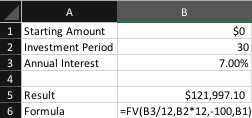
Here’s an example - Let’s say you started today and planned to invest for $100 per year for the next 30 years. The typical stock market return is ~7% per year. This is what the example build would look like.
Notice here the payment is a negative value - this is because the money is coming out of your pocket and going into the investment.
If you wanted to make it $100 per month, you’d divide annual interest by 12 and multiply the 30 years by 12 months. End result -
These two formulas are just the tip of the iceberg when it comes to using excel! If you found this interesting or helpful, leave a comment and I’ll cover some more in the coming weeks.
As a reminder, I’m on a mission to raise $2000 for two charities - the Wounded Warrior Project and the Jump$tart Coalition. WWP helps physically and mentally wounded veterans get the help they need and Jump$tart helps get financial literacy taught in schools. To bring awareness to these two, I’m participating in the Goggins Challenge March 5-7 which involves running 4 miles every 4 hours for 48 hours. If you feel compelled to donate, I have a GoFundMe set up and you can follow the link below. If not, that’s okay! Sharing the post is just as powerful - I’d like to get as many eyes on both charities as possible. Click here!
Talk next week
~Brock
If you are a first-time reader, welcome to the Scuttlebutt! I hope you liked what you read - if you did and want this in your inbox weekly, hit subscribe here!